恒成立问题3种基本方法
恒成立问题是指一个数学命题是否在所有情况下都成立。在数学证明中,恒成立问题是一个常见的难点。以下是三种基本方法来解决恒成立问题。
第一种方法是通过数学归纳法。数学归纳法是一种证明恒成立问题的常用方法。它的基本思想是,如果一个命题在某个起始点成立,并且在某个整数时成立,则它在所有整数时都成立。因此,通过归纳法可以证明一些命题在所有情况下都成立。这种方法最适用于那些可以按顺序排列的问题。
第二种方法是通过反证法。反证法是一种证明恒成立问题的方法,它的基本思想是,假设一个命题不成立,然后推导出一个矛盾的结论,从而证明该命题是恒成立的。这种方法特别适用于那些可以通过逻辑推理证明的问题。
http://jsq.easiu.com/common/images/uacXnonaGa_4.jpg
第三种方法是通过直接证明法。直接证明法是一种证明恒成立问题的常用方法,它的基本思想是,通过一系列逻辑推理,从已知的前提条件出发,证明命题在所有情况下都成立。这种方法适用于那些简单的命题,不需要复杂的逻辑推理。
总之,以上三种方法都是解决恒成立问题的基本方法。在实际应用中,根据具体问题的特点和难点,选择合适的方法进行证明,可以提高证明的效率和准确性。

荣事达royalstar电路图

老板燃气灶维修点大连

格力空调e6维修价格
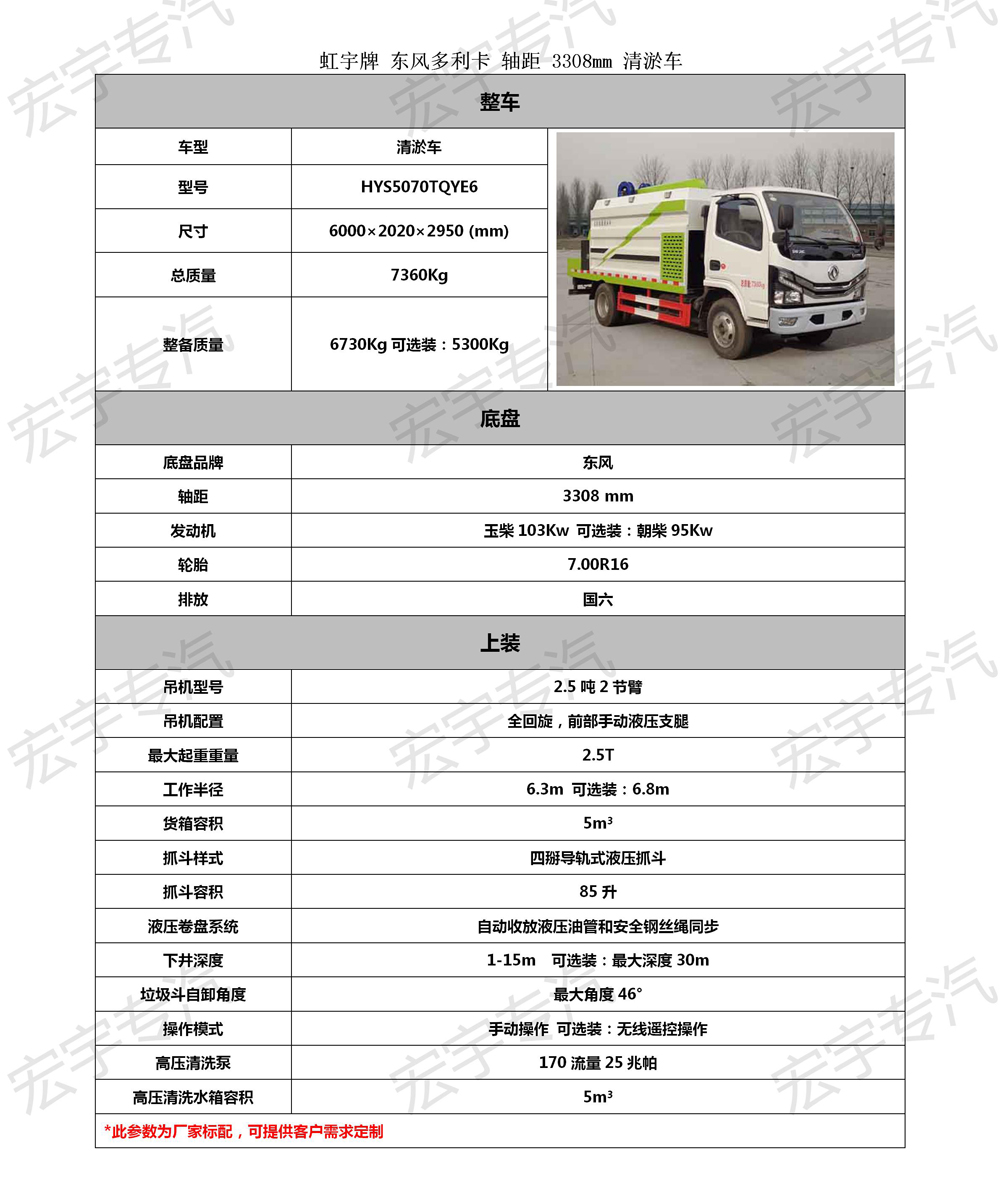
南京苹果售后哪家好

滚筒洗衣机电脑版坏了

海尔小家电报修

变频器开关电源k2225 的工作温度

tcl电视无法全屏

深圳三菱空调是山寨

led47r5200pde固件

开吸油烟机空调就响

彩色电视机图像失真

空调电脑板烧掉

洗衣机启动电容在哪里

空调高压堵塞是什么样现象

清洗中央空调的视频教程

天然气热水器不打火是什么原因

空调浮子开关电阻

led32k10 一亮 就灭

tcl32f1500-3d反复黑屏